Computer Science for CONTINUOUS Data
Motivation
Digital Computers naturally process discrete data, such as
bits or integers or strings or graphs. From bits to advanced data structures,
from a first semi-conducting transistor to billions in wafer-scale integration,
from individual Boolean connectives to entire CPU circuits, from kB to TB
memories, from 10 to 109 instructions per second, from
punched cards to high-level programming languages:
the success story of digital computing arguably is due to (1) hierarchical
layers of abstraction and (2) the ultimate reliability of each layer for the
next one to build on ― for processing discrete data.
Continuous data on the other hand commonly arises in
Physics, Engineering and Science: natura non facit saltus.
Such data mathematically corresponds to real numbers, smooth functions, bounded
operators, or compact subsets of some abstract metric space.
The rise of digital (over analog) computers led a stagnation
in the realm of continuous (=non-discretized) data processing:
35 years after introduction and hardware standardization of IEEE 754 floating
point numbers, mainstream Numerics is arguably still dominated by this forcible
discretization of continuous data ― in spite of violating associative and
distributive laws, breaking symmetries, introducing and propagating rounding
errors, in addition to an involved (and incomplete) axiomatization including
NaNs and denormalized numbers.
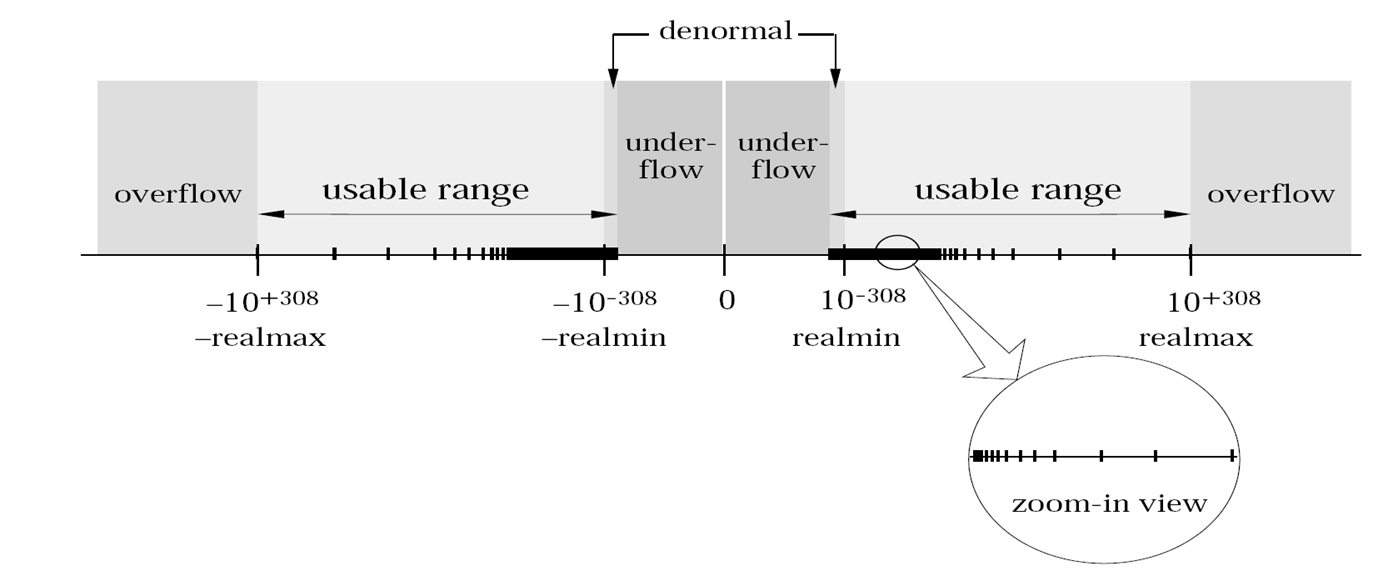
Figure 1: Floating Point Number Line, from https://courses.engr.illinois.edu/cs357/fa2019/assets/images/figs/floatingpoints.png.
See also https://www.jasss.org/9/4/4.html#2.1
Deviations between mathematical structures and their
hardware counterparts are common also in the discrete realm,
such as the “integer” wraparound 255+1=0 occurring in bytes that led to the ”Nuclear Gandhi''
programming bug.
Similarly, deviations between exact and approximate continuous data underlie infamous failures such as the Ariane 501 flight V88 or the Sleipner-A oil platform.
Nowadays high-level programming languages (such as Java
or Python) offer a user data type (called for example BigInt or
mpz_t) that fully agrees with mathematical integers, simulated in
software using a variable number of hardware bytes.
This additional layer of abstraction provides the reliability for advanced
discrete data types (such as weighted or labelled graphs) to build on, as
mentioned above.
A similar approach (operating on approximations of tacitly and adaptively chosen finite precision) allows user programs to process real numbers and
other continuous data types as if exact:
Mission
We develop Computer Science for continuous data, to catch up with the discrete case: from foundations via practical implementation to commercial applications.
In fact some object-oriented software libraries, such as iRRAM or Core III or realLib or Ariadne or Aern, have long been providing
general (=including all transcendental) real numbers as exact encapsulated user
data type.
Technically they employ finite but variable precision approximations: much like
BigInt, but with the added challenge of choosing said precision
automatically and adaptively sufficient for the user program to appear as
indistinguishable from exact reals. This requires a new (namely partial)
semantics for real comparison: formalizing the folklore to “avoid” testing for
equality,
in terms of Kleene's ternary logic.
· Sewon Park in his PhD Thesis has extended that semantics to composite expressions, and further to command sequences aka programs, whose correctness can then be symbolically verified using an extension of Floyd-Hoare Logic; see also [doi:10.46298/lmcs-20(2:17)2024].
· Thus
reliably building on single real numbers leads to higher (but finite) dimensional
data types, such as vectors or matrices.
Sewon Park has designed and
analyzed and implemented a reliable
variant of Gaussian Elimination, in particular regarding pivot search.
Seokbin Lee has designed and
analyzed and implemented a reliable
variant of the Grassmannian,
i.e., the orthomodular lattice of subspaces of
some fixed finite-dimensional Euclidean or unitary vector space.
· Infinite
sequences of real numbers arise as elements of ℓp
spaces; and as coefficients to analytic function germs.
Holger Thies has implemented analytic functions for reliably solving
ODEs and PDEs.
See the references below for this and more continuous data types on GitHub.
Like discrete data, processing continuous data on a digital
computer eventually boils down to processing bits:
finite sequences of bits in
the discrete case, in the continuous case infinite sequences,
approximated via finite initial segments.
Coding theory of discrete data is well-established since Claude Shannon’s
famous work, while Coding Theory of Continuous Data is in development.
For example encoding real numbers via binary
expansion renders addition uncomputable.
·
Matthias Schröder has made important contributions
to the qualitative coding theory of continuous data.
Donghyun Lim in his MSc Thesis has
investigated quantitative properties of encoding abstract (such as function) spaces;
see also [doi:10.1145/3705609]
·
Ivan Koswara and
Gleb Pogudin and
Svetlana Selivanova
have related the bit-complexity intrinsic to approximate solutions of
linear partial differential equations
to discrete complexity classes #P and PSPACE.
This complements earlier investigation of ordinary but non-linear differential equations.
Previous works [doi:10.1137/S0097539794263452] and [doi:10.1145/2189778.2189780] have generalized classical polynomials to higher types, such as operators in analysis, in terms of so-called second-order polynomials. The degree subclassifies ordinary polynomial growth into linear, quadratic, cubic etc.
· In order to similarly classify second-order polynomials, [arXiv:2305.03439] defines their degree to be an 'arctic' first-order polynomial (namely a term/expression over variable D and operations + and × and max). This degree turns out to transform as nicely under (now two kinds of) polynomial composition as the ordinary one. We also establish a normal form and semantic uniqueness for second-order polynomials. Then we define the degree of a third-order polynomial to be an arctic second-order polynomial, and establish its transformation under three kinds of composition.
·
Franz
Brauße
and Pieter
Collins envision a
Computer AlgebraAnalysis System
· Klaus Meer initiates Software Testing in Computable Analysis
References
· 35h online lecture series http://youtube.com/playlist?list=PLvcvykdwsGNE9HyG46aT6aqCvvJBZgKZh in YouTube channel
.· C++ classes for continuous data types: https://github.com/realcomputation, https://github.com/holgerthies
· Vision paper [doi:10.1007/978-3-031-14788-3_5]
· Recent publication characterizing the bit-complexity of Partial Differential Equations in terms of discrete complexity classes P/NP/#P/PSPACE/EXP: [doi:10.1016/j.jco.2022.101727]
· Publication on quantitative coding theory of continuous data: [doi:10.1145/3705609]
· Preprint on semantics and formal verification of programs processing real numbers exactly with partial semantics of comparison: https://arxiv.org/abs/1608.05787
· Workshop on Computational Knot Theory organized by Alexander Stoimenow
.· Vision paper (in German) about Artificial Intelligence, written jointly with Andrea Reichenberger
.